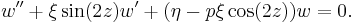Ince equation

In mathematics, the Ince equation, named for Edward Lindsay Ince, is the differential equation

$w^{\prime\prime}%2B\xi\sin(2z)w^{\prime}%2B(\eta-p\xi\cos(2z))w=0. \,$

When p is a non-negative integer, it has polynomial solutions called Ince polynomials.

References

Boyer, Charles P.; Kalnins, E. G.; Jr., W. (1975), "Lie theory and separation of variables. VII. The harmonic oscillator in elliptic coordinates and Ince polynomials", Journal of Mathematical Physics 16: 512–517, ISSN 0022-2488, MR 0372384
Magnus, Wilhelm; Winkler, Stanley (1966), Hill's equation, Interscience Tracts in Pure and Applied Mathematics, No. 20, Interscience Publishers John Wiley & Sons\, New York-London-Sydney, ISBN 978-0-486-49565-1, MR 0197830, http://books.google.com/books?id=ML5wm-T4RVQC
Mennicken, Reinhard (1968), "On Ince's equation", Archive for Rational Mechanics and Analysis (Springer Berlin / Heidelberg) 29: 144–160, ISSN 0003-9527, MR 0223636, http://dx.doi.org/10.1007/BF00281363
Wolf, G. (2010), "Equations of Whittaker–Hill and Ince", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248, http://dlmf.nist.gov/28.31